Je connais Desmos depuis un petit moment, mais je ne m’étais jamais attarder à l’étudier plus intensément. Je dois avouer que je suis un fervent utilisateur de GéoGebra alors, lorsqu’on me propose un nouvel outil, j’ai tendance à me demander : « Pourquoi utiliser ce nouvel outil alors que GeoGebra me convient ? »

En fait la vraie question devrait plutôt être : « Comment cet outil va-t-il aider mes élèves à mieux comprendre la mathématique » C’est dans cet esprit que j’ai entrepris de tester Desmos.

D’abord, je tiens à préciser que j’enseigne la séquence Culture, société et technique en quatrième et cinquième secondaire. Je débute l’année en quatrième avec les fonctions définies par parties et en cinquième je vois le chapitre sur l’optimisation. Disons que ces deux sujets étaient propices à l’exploration.

Dans un premier temps, parlons des fonctions. Quand vient le temps de créer une droite, une parabole, etc. Desmos est très efficace. On écrit l’équation et hop elle apparait! Créer des curseurs ? Facile. En saisissant l’équation y = ax, Desmos nous propose de créer un curseur pour le paramètre a! Et tout ceci dans un interface épuré et intuitif.

Ce que j’aime particulièrement, c’est la possibilité de limiter le domaine (ou l’image) d’une fonction. On entre l’équation de la droite et on limite ensuite le domaine en utilisant un intervalle pour x ou y. GeoGebra nous permet de faire la même chose, mais c’est beaucoup plus compliqué et vraiment moins intuitif.

Commande Desmos : y = 2x + 3 {0 ≤ x < 3}

Commande GeoGebra : Si[0 ≤ x < 3, 2x + 3]

Ces deux commandes vont donner le même résultat dans chacun des outils. Pour un enseignant de mathématique habitué, il n’y a aucune différence, mais pour un élève, Desmos se révèle beaucoup plus simple.

Pour les raisons énumérées plus haut, j’hésitais à utiliser GeoGebra pour ce chapitre. Cette année, j’ai décidé d’intégrer Desmos afin de tracer simplement les fonctions définies par parties. En le faisant, j’ai remarqué que les élèves ont mieux assimilé le concept de valeurs critiques, car ils devaient les trouver s’il voulait tracer les fonctions décrites.

[one-third]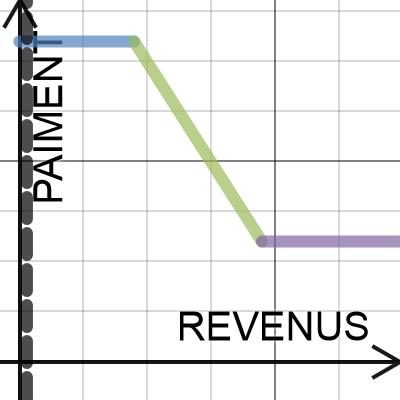
[/one-third] [two-thirds last] Pour les raisons énumérées plus haut, j’hésitais à utiliser GeoGebra pour ce chapitre. Cette année, j’ai décidé d’intégrer Desmos afin de tracer simplement les fonctions définies par parties. En le faisant, j’ai remarqué que les élèves ont mieux assimilé le concept de valeurs critiques, car ils devaient les trouver s’il voulait tracer les fonctions décrites.
[/two-thirds]

Dans un deuxième temps, parlons des polygones de contraintes vue en cinquième secondaire. Pour ce qui est de tracer un demi-plan, Desmos et GeoGebra se comparent. Depuis la dernière année, GeoGebra a développé une version Web qui se rapproche énormément de Desmos.  Malgré cela, j’ai tout de même testé Desmos avec mes élèves.

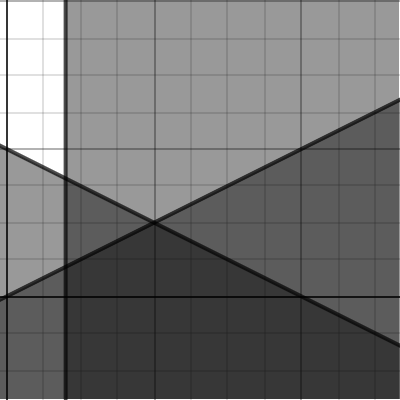
Écrire une inéquation est un jeu d’enfant. Cependant, lorsqu’on entre plusieurs inéquations dans le but de former un polygone de contraintes, on se perd assez rapidement, car Desmos utilise des couleurs différentes pour chacune des inéquations. Assez difficile de se retrouver et de cerner le polygone. Ce problème peut être déjoué lorsqu’on change les couleurs de celles-ci pour toutes les mettre noire par exemple.

[one_half]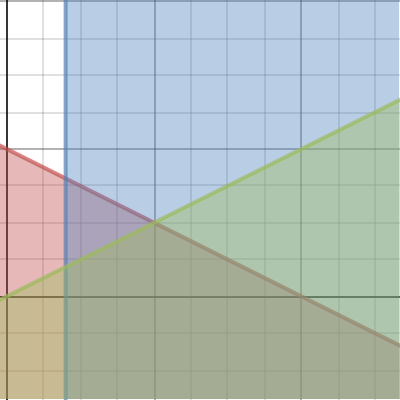
[/one_half] [one_half_last]
[/one_half_last]

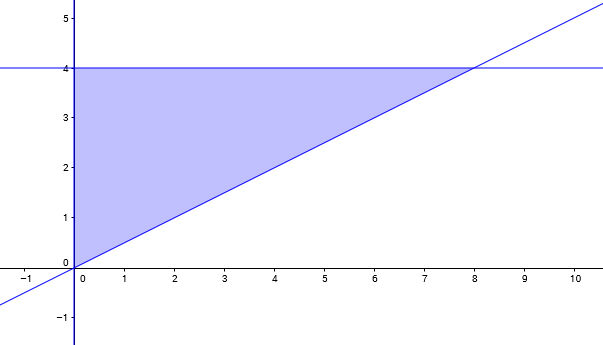
Par défault, GéoGebra utilise la même couleur pour tous les demi-plan. De ce fait, on voit bien le polygone sans avoir à rien modifier. De plus, il est possible de saisir plusieurs inéquations dans la zone de saisie en les séparant par « && » de sorte que seul le polygone apparaisse. Cette fonctionnalité est très intéressante et seul GeoGebra le fait pour le moment.

Commande GeoGebra : x>=0&&y>=0.5x&&y<=4

En conclusion, j’ai bien aimé Desmos pour la simplicité, l’ergonomie, la possibilité d’enregistrer les créations dans le nuage et les récupérer facilement. Je vais probablement continuer à l’utiliser en quatrième secondaire. Pour les polygones de contraintes, je vais plutôt arrêter mon choix sur GéoGebra l’an prochain.