Fonctions périodiques
Exemple de problème
Voici a représentation de la fonction périodique f. En observant le comportement de celle-ci, détermine la valeur de f(8,4).
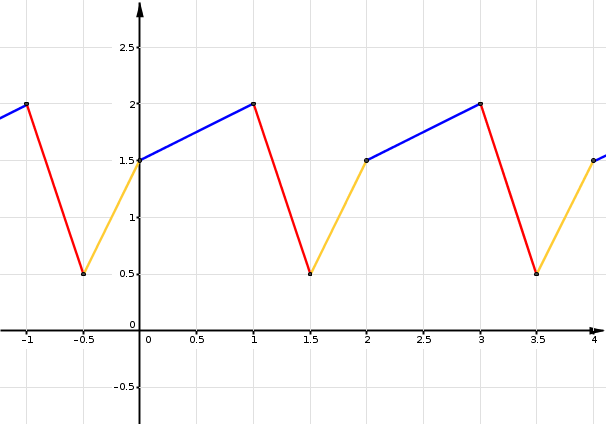
D’abord, lorsque je te demande f(8,4), c’est comme si je te demandais de calculer la valeur de y lorsque x vaut 8,4.
Maintenant, observons l’évolution du graphique. La longueur de la période est 2 et compte trois sections : bleu, rouge et orange. Le nombre de sections importe peu. J’ai mis des couleurs uniquement pour t’aider à bien visualiser le graphique et je vais m’y référer par la suite.
La question que l’on doit se poser est : « Sur quelle section du graphique nous allons tomber lorsque x sera égal à 8,4? ».
La réponse à cette question est la bleue, car cette partie du graphique débute à 0, 2, 4, etc. Donc, on peut très bien s’imaginer qu’elle aura un départ à 8. De plus, elle se termine à 1, 3, 5. On peut aussi s’imaginer qu’elle se termine à 9. Que retrouve-t-on entre 8 et 9 ? 8,4!
Tu pensais que c’était fini? Eh bien non! Tu dois maintenant trouver l’équation associé à ce segment.
On peut déduire les coordonnées des extrémités du segment, puis-ce que cette fonction est périodique et ensuite trouver l’équation associée : (8 ; 1,5) et (9 ; 2)
Équation : f(x) = 0,5x – 2,5
Donc, f(8,4) = 0,5*8,4 – 2,5 = 1,7

